Exame Resolvido Física -UEM-2014- 21 a 30
21. A \(ddp\) entre \(A\) e \(B\) no circuito da figura é de \(12 V\), a intensidade da corrente que flui de \(A\) até \(B\) é de \(6A\). Neste caso o valor de \(R\) é: 
Solução:
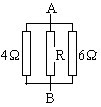
Dado que as 3 resistência estão ligadas em paralelo, então a tensão que passa por cada uma delas será igual a tensão total e a intensidade total será igual ao somatório das intensidades de corrente que passa por cada uma das resistências que compõem o circuito.
Agora, digamos que \(I_1\) é a intensidade que passa pela resistência de \(R_1=4Ω\), e \(I_2\) a que passa por \(R\), e \(I_3\) a que passa pela resistência de \(R_3=6Ω\).
Assim,
\(I_1=\dfrac{U}{R_1}\) \(=\dfrac{12V}{4Ω}\) \(=3A\).
\(I_3=\dfrac{U}{R_3} \) \(=\dfrac{12V}{6Ω}\) \(=2A\).
Dai que:
\(I_1+I_2+I_3=6A\) \(\Rightarrow 3A+I_2+2A=6A\) \(\Rightarrow I_2=1A\).
Entretanto, \(R=\dfrac{U}{I_2}\) \(\Rightarrow R=\dfrac{12V}{1A}\) \(R=12Ω\).
Solução:
Pela Lei de Wien temos que \(\lambda_{máx}=\dfrac{b}{T}\), onde:
\(\lambda_{máx}\), é o comprimento de onda máxima;
\(T\) é a temperatura em Kelvin;
\(b\), é a constante de dispersão de Wien.
Dado que a temperatura da pele humana é de aproximadamente \(35ºC=(273+35)K=308K\), teremos:
\(\lambda_{máx}=\dfrac{3\cdot 10^{-3}m\cdot K}{308K}\) \(=0,00974 \cdot 10^{-3}m\) \(=9,74\cdot 10^{-6}m\).
Solução:
Nesta questão também vamos aplicar a Lei de Wein:
\(\lambda_{máx}=\dfrac{b}{T}\) \(=\dfrac{2,9\cdot 10^{-3}m\cdot K}{1177ºC}\) \(=\dfrac{2,9\cdot 10^{-3}m\cdot K}{(1177+273)K}\) \(=\dfrac{2,9\cdot 10^{-3}m\cdot K}{1450K}\) \(=0,002\cdot 10^{-3}m\) \(=0,002\cdot 10^{-3} \cdot 10^{-6} \cdot 10^6m\) \(=2000\cdot 10^{-9}m\) \(=2000 nm\).
Solução:
Sabendo que \(\lambda=\dfrac{c}{f}\) \(\Rightarrow f=\dfrac{c}{\lambda}\).
Entretanto, \(f=\dfrac{3\cdot 10^5km/s}{200 m}\) \(=\dfrac{3\cdot 10^5\cdot 10^3m/s}{200m}\) \(=0,015\cdot 10^8Hz\) \(=1,5\cdot 10^6Hz\).
Solução:
Para resolver esta questão vamos mais uma vez aplicar a Lei de Wein:
\(\lambda_{máx}=\dfrac{b}{T}\) \(=\dfrac{3\cdot 10^{-3} K\cdot m}{1000K}\) \(=\dfrac{3\cdot 10^{-3} K\cdot m}{10^3K}\) \(=3\cdot 10^{-6}m\).
Solução:
Como \(E=h\cdot f\) e \(\lambda=\dfrac{c}{f}\) \(\Rightarrow f=\dfrac{c}{\lambda}\) então:
\(E=h\cdot \dfrac{c}{\lambda}\) \(=4,14\cdot 10^{-15}eV.s\cdot \dfrac{300000 km/s}{589 nm}\) \(=4,14\cdot 10^{-15}eV.s\cdot \dfrac{3\cdot 10^8m/s}{589\cdot 10^{-9}m}\) \(=0,021\cdot 10^{-15+8+9}eV\) \(=0,021\cdot 10^{2}eV\) \(=2,1eV\).
NOTA: No enunciado \(h=4,14\cdot 10^{15}eV.s\) mas esta incorrecto. O valor correcto é \(h=4,14\cdot 10^{-15}eV.s\).
Solução:
Sabendo que \(\dfrac{A_o}{A}=2^{\frac{t}{t_{1/2}}}\), onde:
\(A_o=40g\), é a massa inicial;
\(A=5g\), é a massa final;
\(t=63h\), é o tempo decorrido;
\(t_{1/2}=?\), é a vida-média.
Assim, \(\dfrac{40g}{5g}=2^{\dfrac{63h}{t_{1/2}}}\) \(\Rightarrow 8=2^{\dfrac{63h}{t_{1/2}}}\) \(\Rightarrow 2^3=2^{\dfrac{63h}{t_{1/2}}}\) \(\Rightarrow 3=\dfrac{63h}{t_{1/2}}\) \(\Rightarrow 3\cdot t_{1/2}=63h\) \(\Rightarrow t_{1/2}=\dfrac{63h}{3}\) \(\Rightarrow t_{1/2}=21h\).
Solução:
Na reacção \( _Z^AX \rightarrow _{Z-2}^{A-4}Y\) temos um decaimento \(α\), porque o átomo \(X\) diminui \(4\) unidades de massa e \(2\) de número atómico.
Na reacção \( _{Z-2}^{A-4}Y \rightarrow _{Z-2}^{A-4}Y\) temos um decaimento \(γ\), porque o átomo \(Y\) não a sua massa nem o número atómico.
Na reacção \( _{Z-2}^{A-4}Y \rightarrow _{Z-1}^{A-4}K \) temos um decaimento \(β\), porque a massa mantém-se mas o número atómico diminui e uma unidade.
Solução:
Sabendo que um núcleo ao emitir uma partícula \(α\), o seu número atómico diminui de duas unidades e o seu número de massa diminui em quatro unidades:
Assim teremos, \( X_{84}^{210} \rightarrow Y_{84-2}^{2010-4} + \alpha \).
Entretanto, número de massa do elemento \(Y\) é \(206\).
Solução:
Ao completarmos a reacção temos:
\( _{92}^{235}X+_0^1n \rightarrow _{55}^{138}Y+_{39}^{95}Z+3(_0^1n)+2( _{-1}^0β )+Q \).
Entretanto, \(bx\) representa 2 electrões.
Comentários
Enviar um comentário