Exame Resolvido de Física-12ª 1ªÉpoca 2011 - 1 à 10
Solução:
Por definição a velocidade média escalar é igual a distância total percorrida sobre o tempo gasto no percurso, e escreve-se \( v_m=\frac{d}{t}\).
Agora, como o automóvel fez o seu percurso com velocidades diferentes em dois intervalos de tempo, então vamos achar a distância percorrida em cada intervalo de tempo.
De \(0\) à \( 45min\): \(t_1= 45min\) \(=45min\cdot \dfrac{1h}{60min}\) \(=0,75h\) e \( v_1=80km/h\)
Assim, \( d_1=v_1 \cdot t_1 \) \(=80km/h \cdot 0,75h\) \(=60km\).
De \(45min\) à \(60min\): \(t_2=15min\) \(=15min \cdot \dfrac{1h}{60min}\) \(=0,25h\) e \(v_2=60km/h\)
Assim, \( d_2=v_2 \cdot t_2 \) \(=60km/h \cdot 0,25h\) \(=15km\).
Daí que a distância total percorrida pelo automóvel é \(d=d_1+d_2\) \(=60km+15km\) \(=75km\).
Entretanto, a velocidade escalar média é \(v_m=\dfrac{d}{t}=\dfrac{75km}{1h}=75km/h\).
Solução:
Ao analisar a figura podemos constatar que do instante \(t=2s\) à \( t=5s\) o ponto material move-se em movimento uniforme, sendo assim, a velocidade é constante nesse mesmo intervalo e é dada pela inclinação do gráfico, isto é: \[ v=\frac{\Delta s}{\Delta t}=\frac{1m-4m}{5s-2s}=\frac{-3m}{3s}=-1m/s\]
Entretanto, a velocidade procurada do ponto material no instante \( t=3s\) é \(-1m/s\) pois ela é constante em no intervalo de \( 2s\) à \(5s\).
Solução:
Sabendo que a equação da altura é dada por:
\begin{equation} h=\frac{1}{2}gt^2 \end{equation}
Então, primeiro devemos calcular o tempo. Para tal aplicamos a seguinte fórmula: \( v_f=v_0+gt\).
Assim, \(10m/s=\cancelto{0}{v_0}+10m/s^2 \cdot t\) \(\Rightarrow t=\frac{10m/s}{10m/s^2}=1s\).
Agora, substituindo \( t=1s\) na equação (1), teremos:
\(h=\frac{1}{2}\cdot 10m/s^2 \cdot (1s)^2\) \(=5m\).
Solução:
Sabendo que o momento é definido pela relação \( M=F\cdot d\), então podemos concluir que:
\( M_1=F_1\cdot d_1\) \(=5N \cdot 2m\) \(=10N\cdot m\) e
\( M_2=F_2\cdot d_2\) \(=80N \cdot 10cm\) \( =80N \cdot 0,1m\) \(=8N \cdot m\).
Sendo assim, o módulo do momento resultante será dado pelo módulo da diferença entre \(M_1\) e \( M_2\) visto que as forças aplicadas na porta tem sentidos opostos.
Entretanto, \(M_r=|M_1-M_2|=2N\cdot m\).
Solução:
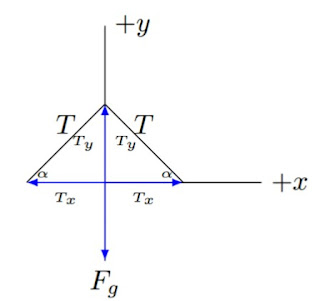
Podemos interpretar a questão atraves do esquema da figura seguinte:
Logo, facilmente chegamos a conclusão que para o quadro se manter pendurado (em equilíbrio) é necessário que:
\(T_y+T_y=P\) \( \Rightarrow 2T\cdot \mathrm{sen}30° =m\cdot g \) \( \Rightarrow 2T\cdot \frac{1}{2}=3kg\cdot 10m/s^2\) \(\Rightarrow T=30N\).
Solução:
Como a equação é do tipo \( x=x_0 + v_0t + \frac{1}{2}at^2\) então teremos que \( \frac{1}{2}at^2=t^2\) \( \Rightarrow a=\frac{2t^2}{t^2}\) \( \Rightarrow a=2m/s^2\).
Entretanto, \( F=m\cdot a\) \(= 6kg \cdot 2m/s^2\) \(=12N\).
Solução:
Visto que depois de colidirem entre si os blocos movem-se juntos como se fossem um único corpo, então trata-se de uma colisão perfeitamente inelástica.
Daí que apenas ocorrerá a conservação do momento linear. Isto é:
\(m_A\cdot v_A-m_B\cdot v_B=(m_A+m_B)\cdot v_{AB} \) \( \Rightarrow v_{AB}=\frac{m_Av_A-m_Bv_B}{m_A+m_B}\) \(=\frac{2m\cdot 11m/s-m\cdot 4m/s}{2m+m}\) \(=\frac{22m-4m}{3m}m/s\) \(=\frac{18m}{3m}m/s\) \(=6m/s\).
Solução:
A medida que a mola se comprime a energia cinética do bloco vai diminuindo e a energia potencial elástica aumenta até se equilibrarem.
Portanto, quando a deformação é de \( x=0,4m\), teremos que:
\( E_c=E_{pl}\) \( \Rightarrow \frac{1}{2}mv^2=\frac{1}{2}kx^2\) \( \Rightarrow v^2=\frac{kx^2}{m}\) \( \Rightarrow v=\sqrt{\frac{kx^2}{m}}\) \(\Rightarrow v=\sqrt{\frac{6N/m \cdot (0,4m)^2}{1,5kg}}\) \( \Rightarrow v=\sqrt{0,64}m/s\) \( \Rightarrow v=0,8m/s \).
Solução:
Para que a carga \(q\) permaneça em repouso é necessário que a força \(F_M\) provocada pela carga \(Q_M\) sobre a carga \(q\) e a força \( F_N\) provocada pela carga da partícula \(N\) sobre a carga \(q\), sejam iguais, isto é:
\(\frac{k\cdot Q_M \cdot q}{x^2}=\frac{k\cdot Q_N \cdot q}{(1-x)^2}\) \( \Rightarrow \frac{k\cdot Q_M \cdot q}{x^2}-\frac{k\cdot 9Q_M\cdot q}{1-2x+x^2}=0\) \(\Rightarrow k\cdot Q_M\cdot q (\frac{1}{x^2}-\frac{9}{1-2x+x^2})=0\) \( \Rightarrow \frac{1}{x^2}-\frac{9}{1-2x+x^2}=0\) \( \Rightarrow 1-2x+x^2-9x^2=0\) \( \Rightarrow -8x^2-2x+1=0\) \( \Rightarrow 8x^2+2x-1=0\).
Depois de resolver esta equação quadrática vamos encontrar \( x=0,25 \vee x=-0,5\). Entretanto, a distância deverá ser de \(0,25m\) pois tratando-se de uma distância ela não pode ser negativa.
Solução:
O potencial eléctrico que atua num ponto é igual ao somatório de cada potencial eléctrico que atua sobre esse ponto, neste caso é da por: \( V=\frac{k\cdot q_1}{d_1}+\frac{k\cdot q_2}{d_2}\) \( \Rightarrow V=\frac{9\cdot 10^9Nm^2/C^2\cdot (-30\cdot10^{-6}C)}{3\cdot 10^{-1}m}+\frac{9\cdot 10^9Nm^2/C^2\cdot 40\cdot10^{-6}C}{3\cdot 10^{-1}m}\) \(=-9\cdot 10^5V+12\cdot 10^5V\) \(=3\cdot 10^5 V\).

Comentários
Enviar um comentário