Exame Resolvido Física -UEM-2014- 31 a 40

Ir para: 1-10 | 11-20 | 21-30 |

31. $_1^3A + _1^2B \rightarrow _2^4C + _0^1D$ Na reacção de fusão, a partícula $D$ é chamada:

Solução:
A partícula $D$ é chamada Neutrão porque tem uma unidade de numero de massa atómica e zero unidades de numero atómico.

32. Uma superfície metálica, cuja função trabalho é $2 eV$, é iluminada por fotões de energia de $3 eV$. Qual é, em $eV$, a energia cinética máxima dos fotões emitidos por esta superfície?

Solução:
De acordo com Einstein, a energia cinética máxima dos fotões emitidos deve ser a diferença entre a energia dos fotões incidente e a função trabalho do material. Isto é, $E_c=E-\Phi$ $=3eV-2eV$ $=1eV$.

33. Num lago de água doce, a pressão hidrostática depende da profundidade $h$ do mesmo. O esboço gráfico correcto de $P\times h$ no lago é:

Solução:
Pelo principio Fundamental da Hidrostática temos que:
"A diferença de pressão entre dois pontos do mesmo liquido é igual ao produto da massa especifica (densidade) pelo modulo da aceleração de gravidade local e pela diferença de profundidade entre os pontos considerados".

Assim, $P_f-P_o=\rho \cdot g \cdot h$ $\Rightarrow P_f=P_o+\rho \cdot g \cdot h$.

Logo, podemos concluir que a pressão aumenta com o aumento da profundidade.

Entretanto, o esboço gráfico correcto de $P\times h$ no lago é o da alínea $E$.

34. Uma torneira enche de água um tanque, cuja capacidade é de $6000 litros$, em $1 h$ e $40 min$. Qual é, em unidades SI, a vazão da torneira?

Solução:
$Q=\dfrac{V}{t}$, onde:
$Q=?$, é a vazão da torneira;
$V=6000l$, é o volume da água;
$t=1h+40min$, é o tempo necessário para encher o tanque.

Assim, $Q=\dfrac{6000l}{1h+40min}$ $=\dfrac{6m^3}{3600s+2400s}$ $=\dfrac{6m^3}{6000s}$ $=0,001m^3/s$ $=10^{-3}m^3/s$.

35. Numa cultura irrigada por um cano que tem a área de secção recta de $100 cm^2$ passa água com uma vazão de $7200$ litros por hora. A velocidade de escoamento da água, em unidades SI, nesse cano é:

Solução:
$Q=7200l/h$ $=\dfrac{7200l}{1h}$ $=\dfrac{7200\cdot 10^{-3}m^3}{3600s}$ $=2\cdot 10^{-3}m^3/s$.

Agora, sabendo que a vazão também pode ser expressa por $Q=S\cdot v$, onde:
$S=100cm^2$, é a área de secção recta;
$v=?$, é a velocidade de escoamento da água.

Assim, $Q=S\cdot v$ $\Rightarrow v=\dfrac{Q}{S}$ $=\dfrac{2\cdot 10^{-3}m^3/s}{100cm^2}$ $=\dfrac{2\cdot 10^{-3}m^3/s}{(10cm)^2}$ $=\dfrac{2\cdot 10^{-3}m^3/s}{(0,1m)^2}$ $=\dfrac{2\cdot 10^{-3}m^3/s}{0,01m^2}$ $=\dfrac{2\cdot 10^{-3}m^3/s}{10^{-2}m^2}$ $=2\cdot 10^{-1}m/s$.

36. O sangue circula a $30 cm/s$ numa artéria aorta com $9 mm$ de raio. Qual é, em litros por minuto, a vazão do sangue?

Solução:
$Q=S\cdot v$ $=\pi\cdot r^2\cdot v$ $=\pi\cdot (9mm)^2\cdot 30cm/s$ $=\pi\cdot (9\cdot 10^{-3}m)^2\cdot 30\cdot 10^{-2}m/s$ $=3,14\cdot 81\cdot 10^{-6}m^2\cdot 30\cdot 10^{-2}m/s$ $=7630,2\cdot 10^{-8}m^3/s$ $=\dfrac{7630,2\cdot 10^{-5}\cdot 10^{-3}m^3\cdot 60}{60s}$ $=\dfrac{457812\cdot 10^{-5}l}{1min}$ $=\dfrac{4,57812l}{1min}$ $=4,6l/m$.

37. Uma certa quantidade de gás ideal ocupa um volume $V_0$ quando sua temperatura é $T_0$ e sua pressão é $P_0$. O gás expande-se isotermicamente até duplicar o seu volume. A seguir, mantendo o seu volume constante, sua pressão é restabelecida ao valor original $P_0$. Qual a temperatura final do gás neste último estado de equilíbrio térmico?

Solução:
1ª Etapa:
Como o gás expande-se isotermicamente então a temperatura é constante ($T_o=T_1$):
Assim, $\dfrac{P_o\cdot V_o}{T_o}=\dfrac{P_1\cdot V_1}{T_o}$ $\Rightarrow P_o\cdot V_o=P_1\cdot V_1$ $\Rightarrow P_o\cdot V_o=P_1\cdot 2V_o$
$\Rightarrow P_o=2P_1$ $\Rightarrow P_1=\dfrac{P_o}{2}$.

2ª Etapa:
Agora matam-se o volume constante ($V_1=V_2$) e sua pressão é restabelecida ao valor original ($P_2=P_0$):
Assim, $\dfrac{P_1\cdot V_1}{T_1}=\dfrac{P_2\cdot V_1}{T_2}$ $\Rightarrow \dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}$ $\Rightarrow \dfrac{\frac{P_o}{2}}{T_1}=\dfrac{P_o}{T_2}$ $\Rightarrow \dfrac{P_o}{2T_1}=\dfrac{P_o}{T_2}$ $\Rightarrow T_2=2T_1$ $\Rightarrow T_2=2T_o$.

38. A transformação de um certo gás ideal, que recebeu do meio exterior $100 \ calorias$, está representada no gráfico ao lado. Qual é, em joules, a variação da sua energia interna? ( $1 cal = 4 J$ )

Solução:
$\Delta U=Q-W$, onde:
$\Delta U=?$, é a variação da sua energia interna;
$Q=100cal$, é a energia que recebeu do meio exterior;
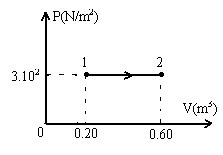
$W$, é o trabalho realizado que é determinado através da área correspondente a transformação.

Assim, $\Delta U=100cal-3\cdot 10^2N/m^2(0,6m^3-0,2m^3)$ $=100\cdot 4J -3\cdot 10^2N/m^2\cdot 0,4m^3$ $=400J -1,2\cdot 10^2N.m$
$=400J-120J$ $=280J$.

39. Uma dada massa de um gás perfeito num recipiente de $8 litros$ de volume, à temperatura de $280 K$, exerce a pressão de $4 atm$. Reduzindo o volume para $6 litros$ e aquecendo o gás, a sua pressão passou a ser $10 atm$. A que temperatura, em $K$, o gás foi aquecido

Solução:
Como $P\cdot V=n\cdot R\cdot T$, então: $\dfrac{P\cdot V}{T}=n\cdot R$, onde $n\cdot R=constante$.

Assim, $\dfrac{P\cdot V}{T}=\dfrac{P_f\cdot V_f}{T_f}$ $\Rightarrow T_f=\dfrac{P_f\cdot V_f \cdot T}{P\cdot V}$ $\Rightarrow T_f=\dfrac{10atm\cdot 6l \cdot 280K}{4atm\cdot 8l}$ $\Rightarrow T_f=525K$.

40. Durante a expansão, um determinado gás recebe $Q=200 J$ de calor e realiza $w=140 J$ de trabalho. No fim do processo, pode-se afirmar que a energia interna do gás:

Solução:
$\Delta U=Q-W$, onde:
$\Delta U=?$, é a variação da sua energia interna;
$Q=200J$, é a energia que recebeu do meio exterior;
$W=140J$, é o trabalho realizado.

Assim, $\Delta U=200J-140J$ $=60J$.

Entretanto, a energia interna do gás aumentou em $60J$.

Nota: Se $\Delta U$ for negativa, significa que a energia interna diminuiu.

Ir para: 1-10 | 11-20 | 21-30 |