Exame Resolvido Física-Extra-12a-2014-31-40

Ir para: 1-10 | 11-20 | 21-30

31. Um fluído escoa por um cano uniforme de 8cm de diâmetro a uma velocidade média de \(3m/s\). Qual é, em \(m^3/s\), a respectiva vazão?

Solução:
Sabendo que a vazão é dada por: \(Q=S \cdot v\), onde \(Q\) é a vazão, \(S\) é a secção e \(v\) é a velocidade.
Então teremos, \(Q=\pi r^2 \cdot v\). Como o raio é igual a metade do diamentro, teremos, \(Q=\pi \cdot \left(\dfrac{d}{2}\right)^2\cdot v\) \(=\pi \cdot \left(\dfrac{8cm}{2}\right)^2\cdot 3m/s\) \(=3,14 \cdot \left(\dfrac{0,08m}{2}\right)^2\cdot 3m/s\) \(=3,14 \cdot (0,04m)^2\cdot 3m/s\) \(=1,5072\cdot 10^{-2}m^3/s\).

32. A figura representa três secções transversais de uma tubulação horizontal afunilada, por onde se escoa um fluído. Qual é a relação entre as vazões nas secções (1) , (2) e (3)?

Solução:
Como base na equação de continuidade podemos dizer que \(Q_1=Q_2=Q_3\).

33. Num tubo horizontal de diâmetro \(D_1\) passa uma corrente de água a uma velocidade de \(10m/s\). O diâmetro do tubo, a partir de um certo ponto, fica reduzido a metade do inicial. Qual é, em \(m/s\), a velocidade neste estreitamento do tubo de diâmetro \(D_2\)?

Solução:
\(Q=\pi \left(\dfrac{d_1}{2}\right)^2 \cdot v_1=\pi \left(\dfrac{d_2}{2}\right)^2 \cdot v_2\) \(\Rightarrow \pi \left(\dfrac{d_1}{2}\right)^2 \cdot 10m/s=\pi \left(\dfrac{\frac{d_1}{2}}{2}\right)^2 \cdot v_2\) \(\Rightarrow \pi \left(\dfrac{d_1}{2}\right)^2 \cdot 10m/s=\pi \dfrac{\left(\frac{d_1}{2}\right)^2}{4} \cdot v_2\) \(\Rightarrow v_2=\dfrac{\pi \left(\dfrac{d_1}{2}\right)^2 \cdot 10m/s}{\pi\dfrac{\left(\frac{d_1}{2}\right)^2}{4}}\) \(=\pi \left(\dfrac{d_1}{2}\right)^2 \cdot 10m/s \cdot \dfrac{4}{\pi \left(\frac{d_1}{2}\right)^2}\) \(=10m/s \cdot 4\) \(=40m/s \).

34. Qual é, em \(Joules\), a variação da energia interna de um gás ideal sobre o qual é realizado um trabalho de \(120J\), durante uma compressão isotérmica?

Solução:
Como a energia interna de um gás ideal depende exclusivamente da sua temperatura então podemos afirmar que a variação da energia interna será igual a zero (\(\Delta U=0\)), porque trata-se de uma compressão isotérmica, isto é, a temperatura é constante (não varia).

35. Um cilindro contém 0,100 mol de um gás ideal monoatómico. No estado inicial o gás está sob pressão de \(l \cdot 10^5Pa\) e ocupa um volume igual a \(2,5\cdot 10^{-3}m^3\). Se o gás se expande isotermicamente até ao dobro do seu volume inicial, qual é, em \(kelvin\), a sua temperatura final? (\(R = 8,31 SI\))

Solução:
Sabendo que: \(p\cdot V=n\cdot R\cdot T\), entao, \(T=\dfrac{pV}{nR}\) \(=\dfrac{1\cdot 10^5Pa\cdot 2,5 \cdot 10^{-3}m^3}{0,100mol\cdot 8,31}\) \(=\dfrac{2,5\cdot 10^2}{0,831}\) \(=\dfrac{250}{0,831}\) \(=300,8K\).

36. Um gás ideal vai do estado \(M\) até ao estado \(N\) ao longo de uma linha recta no diagrama PV. Qual é, em \(Joules\), o trabalho realizado pelo gás neste processo?

Solução:
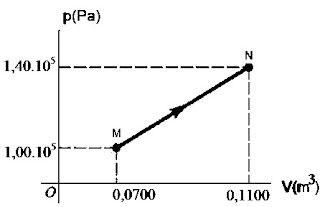
Como o trabalho realizado é definido pelo area correspondente ao grafico \(p X V\); Veja a figura abaixo:

Então, \(T=A_1+A_2\) \(=\dfrac{(p_2-p_1)(V_2-V_1)}{2} + p_1(V_2-V_1)\) \(=\dfrac{(1,40\cdot 10^5-1,00\cdot 10^5)(0,1100-0,0700)}{2} + 1,00\cdot 10^5(0,1100-0,0700)\) \(=\dfrac{0,4\cdot 10^5 \cdot 0,04}{2}+1\cdot 10^5\cdot0,04\) \(=0,2\cdot 10^5 \cdot 0,04+1\cdot 10^5\cdot0,04\) \(=1,2\cdot 10^5 \cdot 0,04\) \(=0,048\cdot 10^5\) \(=4,8\cdot 10^3J\).

37. A posição de uma partícula que realiza movimento oscilatόrio é dada por \(x= 4cosπt \)( SI ). Qual é, em \(m/s\), a velocidade da partícula no instante \(t=0,5s\)?

Solução:
Para resolver este exercício devemos conhecer a equação da velocidade do movimento oscilatório:
\(v(t)=-\omega A \cdot \mathrm{sen}(\omega t+\phi) \).

Assim, \(v(t)\), para \(x(t)\), sera: \(v(t)=-4π\cdot \mathrm{sen}(πt) \).

Entretanto, \(v(0,5)=-4π\cdot \mathrm{sen}(π\cdot 0,5) \) \(=-4π\cdot \mathrm{sen}(\frac{π}{2}) \) \(=-4π\cdot 1 \) \(=-4π\).

38. Qual é, em \(segundos\), o período das oscilações de um pêndulo de mola de constante elástica \(k=12π^2\) (SI), quando nele se pendura uma massa de \(30g\)?

Solução:
\(T=2π\sqrt{\dfrac{m}{k}}\) \(=2π\sqrt{\dfrac{30g}{12π^2}}\) \(=\dfrac{2π}{π}\sqrt{\dfrac{0,030}{12}}\) \(=2\sqrt{0,0025}\) \(=2\cdot 0,05\) \(=0,10s\).

39. O gráfico refere-se às oscilações dum corpo que executa MHS de acordo com a equação: \(y(t) = \dfrac{π}{2}\mathrm{sen}πt\) (SI). Quais são, respectivamente, os valores representados pelas letras \(N\) e \(M\), em unidades SI?

Solução:
Como \(N\) representa a amplitude máxima da oscilação, então: \(N=\dfrac{π}{2}\).

E, \(M\) representa \(\dfrac{3}{4}\) de uma volta completa, isto é, do período das oscilações, entao: \(M=\dfrac{3}{4}\cdot T\) \(=\dfrac{3}{4}\cdot \dfrac{2π}{\omega}\) \(=\dfrac{3}{4}\cdot \dfrac{2π}{π}\) \(=\dfrac{3}{4}\cdot 2\) \(=\dfrac{6}{4}\) \(=1,5\).

40. Seja \(T\) o período de um pêndulo simples de comprimento \(L\), quando colocado num planeta onde a aceleração gravitacional é \(g\). Como variará o período deste pêndulo, se for transportado para a superfície dum planeta onde a aceleração de gravidade é \(9 vezes maior\)?

Solução:
Seja \(T_1=2π \sqrt{\dfrac{L}{g_1}} \) e \(T_2=2π \sqrt{\dfrac{L}{g_2}} \).

Agora, como \(g_1=g\) e \(g_2=9g\), entao:
\(T_2=2π \sqrt{\dfrac{L}{9g}} \) \(=2π \sqrt{\dfrac{L}{g}\cdot \dfrac{1}{9}}\) \(=2π \sqrt{\dfrac{L}{g} } \cdot \sqrt{\dfrac{1}{9}}\) \(=T_1 \cdot \dfrac{1}{3}\) \(=\dfrac{T_1}{3}\).

Entretanto, o período reduzira 3 vezes.

Ir para: 1-10 | 11-20 | 21-30