Exame Resolvido Física-Extra-12ª -2014 - 21 a 30

Ir para: 1-10 | 11-20 | 31-40

21. Qual é, em unidades SI, o comprimento de onda de um fotão de energia $2,5 eV$? ($e = 1,6.10^{-19}C$, $h=7.10^{-34}J.s$, $c=300000 km/s$)

Solução:
$E=h\cdot \dfrac{c}{\lambda}$ $\Rightarrow \lambda=h \cdot \dfrac{c}{E}$ $\Rightarrow \lambda=7.10^{-34}J.s \cdot \dfrac{300000 km/s}{2,5 eV}$ $\Rightarrow \lambda=7.10^{-34}J.s \cdot \dfrac{300000 \cdot 10^3 m/s}{2,5 \cdot 1,6\cdot 10^{-19}C}$ $\Rightarrow \lambda=7.10^{-34}J.s \cdot \dfrac{3 \cdot 10^8 m/s}{4\cdot 10^{-19}C}$ $\Rightarrow \lambda=\dfrac{21 \cdot 10^{-26} m/s}{4\cdot 10^{-19}C}$ $\Rightarrow \lambda=5,25\cdot 10^{-7}m$.

22. A função trabalho do sódio é de $2,3eV$. Qual é, em $eV$, a energia cinética máxima dos fotoelectrões emitidos se a luz de comprimento de onda de $300nm$ incidir sobre uma superfície de sódio?($h=6,625.10^{-34}J.s$; $C=3.10^8m/s;1 nm =10^{-9}m$; $1eV=1,6\cdot 10^{-19}J$)

Solução:
$E_{max}=hf-\Phi$ $=h\cdot \dfrac{c}{\lambda}-\Phi$ $=6,625\cdot 10^{-34}J.s \cdot \dfrac{3\cdot 10^8m/s}{300nm}-2,3eV$ $=6,625\cdot 10^{-34}J.s \cdot \dfrac{3\cdot 10^8m/s}{300 \cdot 10^{-9}m}-2,3eV$ $=6,625\cdot 10^{-34}J.s \cdot \dfrac{3\cdot 10^8m/s}{300 \cdot 10^{-9}m}-2,3eV$ $=6,625\cdot 10^{-19}J-2,3eV$ $=\dfrac{6,625\cdot 10^{-19}}{1,6\cdot 10^{-19}}eV-2,3eV$ $= 4,14eV-2,3eV=1,84eV$.

23. A função trabalho de um certo material é de $3eV$. Qual é, em $Hz$, a frequência da luz incidente se a energia cinética máxima dos fotoelectrões emitidos é de $3,6eV$? ($h = 4,4.10^{-15}eV.s$)

Solução:
$E_{Max}=hf-\Phi$ $\Rightarrow f=\dfrac{E_{Max}+\Phi}{h}$ $=\dfrac{3,6eV + 3eV}{4,4 \cdot 10^{-15}eV \cdot s}$ $=\dfrac{6,6 eV}{4,4 \cdot 10^{-15} eV \cdot s}$ $=1,5\cdot 10^{15}Hz$.

24. No efeito fotoeléctrico, a energia cinética dos fotoelectrões em função da frequência é dada pela expressão: $E_c( f ) = 7.10^{-34}.f – 2,4.10^{-19}$ ( SI). Qual é, em unidades SI, o valor representado por $X$ no gráfico?

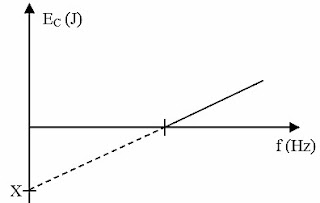
Solução:
Sabendo que a energia cinética dos fotoelectrões em função da frequência é dada pela equação: $E_c=hf-\Phi$, então o valor representado por $X$ no gráfico corresponde a função trabalho, isto é, $\Phi=2,4\cdot 10^{-19}$.

25. O gráfico representa a taxa de decaimento de uma amostra radioativa. Quantos anos são necessários para que a massa da amostra fique reduzida a $3 gramas$?

Solução:

$A=\dfrac{A_0}{2^n}$ $\Rightarrow 2^n=\dfrac{A_0}{A}$ $=\dfrac{96g}{3g}$ $=32$ $\Rightarrow 2^n=2^5$ $\Rightarrow n=5$.

Entretanto, $\Delta t=10\cdot n$ $=10 \cdot 5$ $=50anos$.

26. O que acontece com o número atómico ($Z$) e o número de massa ($A$) de um núcleo radioativo quando ele emite uma partícula alfa?

Solução:
Sabendo que uma emissão de partícula alfa é igual a um núcleo de Hélio que possui uma carga +2 em unidades atómicas e 4 em unidades de massa atómica. Portanto, $Z$ diminui em duas unidades e $A$ diminui em quatro unidades.

27. Na reacção nuclear $^{14}_7N+X \to ^{14}_6C+^1_1H$, $X$ representa um (uma)...

Solução:
Primeiro vamos achar o numero atomico e a massa atomica de $X$:
Assim, $^{14}_7N+^1_0X \to ^{14}_6C+^1_1H$.

Entretanto, $X$, representa um neutrão.

28. Complete a frase:
A equação $X \to ^{222}_{88} Rn +^4_2 y$, representa uma reacção de................................... e as letra $x$ e $y$, ....................................................................................,respectivamente.

Solução:
Determinando o numero atomico e a massa atomica de $X$, temos:
$^{226}_{90}X \to ^{222}_{88} Rn +^4_2 y$.

Entretanto, podemos afirmar que a equação representa uma reacção de desintegração; e as letras $x$ e $y$ representam, o núcleo de $^{226}_{90}Ra$ e uma partícula $\alpha$.

29. Uma amostra radioativa tem um período de semidesintegração de $32 dias$ e uma massa inicial de $800g$. Qual será, em $g$, o valor da massa desta amostra, transcorridos $256 dias$?

Solução:
$A=\dfrac{A_0}{2^n}$ $A=\dfrac{A_0}{2^{\dfrac{t_f}{t_0}}}$ $=\dfrac{800g}{2^{\dfrac{256}{32}}}$ $=\dfrac{800g}{2^8}$ $=\dfrac{800g}{256}$ $=3,125g$.

30. Na fissão de um dado núcleo, o defeito de massa é de $0,4684 u.m.a$. Qual é, em $Mev$, a energia que se liberta durante esse processo? (1uma=931MeV)

Solução:
$E=m \cdot 931 Mev$ $=0,4684 \cdot 931Mev$ $=436,0804Mev$ $=436,01MeV$.

Ir para: 1-10 | 11-20 | 31-40