Resolução 11-19 Exame UEM-2013
Ir para:1-10 | 20-29 | 30-39
Agora, como a área a superfície de uma bola é dada por \(S=4 \pi r^2\) então a razão de proporção das superfícies das duas bolas será dada por: \( \frac{S_1}{S_2}=\frac{4 \pi r_1^{2}}{4 \pi r_2^{2}}\) \( =\frac{\cancel{4 \pi } r_1^{2}}{\cancel{4 \pi} r_2^{2}}\) \( = \frac{r_1^{2}}{r_2^{2}}\) \( = (\frac{ r_1}{r_2})^2\) \( = (\frac{1}{3})^2 \) \( =\frac{1}{9} \).
Assim, \( \frac{x^{49}(2-x)^{51}}{(x^2-3x+2)^{100}} \ge 0 \) \( \Rightarrow \frac{x^{49}(2-x)^{51}}{[(x-1)(x-2)]^{100 }}\ge 0 \).
\(x=0\), \(2-x=0\) \(\Rightarrow x=2\), \(x-1=0\) \(\Rightarrow x=1\) e \(x-2=0\) \(\Rightarrow x=2\).
Depois elaboramos a tabela de variação de sinais.
\(\begin{array}{|c|c|c|c|c|c|c|c|}
\hline
x & ]-\infty; 0[ & 0 & ]0;1[ & 1 & ]1;2[ & 2 & ]2;+\infty[\\
\hline
x^{49} & - & 0 & + & 1 & + & 2^{49} & +\\
\hline
(2-x)^{51} & + & 2^{51} & + & 1 & + & 0 & -\\
\hline
(x-1)^{100} & + & 1 & + & 0 & + & 1 & +\\
\hline
(x-2)^{100} & + & 2^{100} & + & 1 & + & 0 & +\\
\hline
\frac{x^{49}(2-x)^{51}}{(x^2-3x+2)^2} & - & 0 & + & \nexists & + & \nexists & -\\
\hline
\end{array}\)
Entretanto, \( x \in [0;1[ \cup ]1;2[ \).
Agora, como a razão de proporção de meninas e rapazes é \(2:3\), então \( \frac{x}{y} = \frac{2}{3} \) \( \Rightarrow \frac{12}{y} = \frac{2}{3} \), e pela regra de três simples teremos \( y \cdot 2 = 12 \cdot 3 \) \( \Rightarrow y = 18 \).
Entretanto, o número de alunos é \(x+y =12+18 =30 \).
Assim, \(x \sqrt{2-x} \ne 0 \wedge 2-x \gt 0 \) \( \Rightarrow x \ne 0 \vee 2-x \ne 0 \wedge x\lt 2\) \( \Rightarrow x \ne 0 \vee x \ne 2 \wedge x \lt 2 \)
Entretanto, \( x \in ]-\infty; 2[ -\{0;2\} \) \( = ]-\infty; 0[ \cup ]0;2[ \).
Assim, \(x-1 = 0 \wedge 2x+4=0 \wedge 3-x = 0 \) \( \Rightarrow \) \(x=1 \wedge x=-2 \wedge x=3 \).
Em seguida elaborar-se a tabela de variação de sinais de modo a encontrarmos os intervais da solução da inequação.
\(\begin{array}{|c|c|c|c|c|c|c|c|}
\hline
x & ]-\infty; -2[ & -2 & ]-2;1[ & 1 & ]1;3[ & 3 & ]3;+\infty[\\
\hline
x-1 & - & -3 & - & 0 & + & 2 & +\\
\hline
2x+4 & - & 0 & + & 6 & + & 10 & +\\
\hline
3-x & + & 5 & + & 2 & + & 0 & -\\
\hline
\frac{x-1}{(2x+4)(3-x)} & + & \nexists & - & 0 & + & \nexists & -\\
\hline
\end{array}\)
Entretanto, \( x \in ]-\infty;-2[ \cup [1;3[ \).
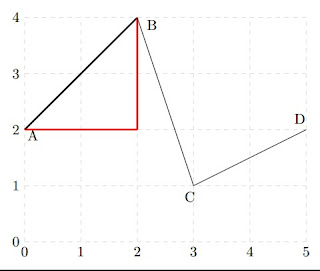
Analisando a figura podemos ver que é possivel criar \(3\) triângulos, onde a hipotenusa de cada um dos triângulos é um dos segmentos de recta que constituem a linha poligonal.
Vamos traçar um triângulo em que a sua hipotenusa seja o segmento de recta \(AB\).
Assim, \(|AB|=\sqrt{2^2+2^2}=2\sqrt{2}\).
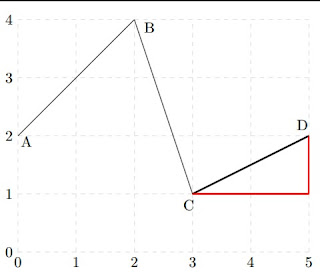
Fazemos o mesmo procedimento para \(BC\) e \(CD\).
\(|BC|=\sqrt{1^2+3^2}=\sqrt{10} \).
\(|CD|=\sqrt{1^2+2^2}=\sqrt{5} \).
Entretanto, o comprimento será igual a \(2\sqrt{2}+\sqrt{10}+\sqrt{5} \).
\( \log_5{(\log_2b)}=0 \) \( \Rightarrow \log_2b = 5^0 \) \( \Rightarrow \log_2b=1 \) \( \Rightarrow b=2^1\) \(\Rightarrow b=2 \).
Daí que \( a+b=5+2=7\).
Então, \(a_{11}\) é o termo médio e \(a_{10}\) é o seu antecedente.
Assim, \(a_{11}+a_{10} = a_{21} \) \(\Rightarrow a_1+10d + a_1+9d=a_1+20d\) \(2a_1+10\cdot 7 + 9\cdot 7= a_1 + 20 \cdot 7\) \(\Rightarrow 2a_1-a_1 = 20 \cdot 7 - 19 \cdot 7 \) \(\Rightarrow a_1=7\).
Entretanto, \( a_{21}=a_1+20d=7+20 \cdot 7=147\).
Ir para:1-10 | 20-29 | 30-3911. Se a relação dos volumes de duas bolas é \(1:27\), então a relação das superfícies destas bolas é:
Resolução:
Sabendo que o volume de uma bola é dada por \(V=\frac{4}{3}\pi r^3\), e como a razão de proporcionalidade entre duas bolas é \(1:27\). Então, teremos que \(\frac{V_1}{V_2}=\frac{1}{27}\) \(\Rightarrow \frac{\frac{4}{3}\pi r_1{^3}}{\frac{4}{3}\pi r_2^{3}}=\frac{1}{3^3}\) \(\Rightarrow \frac{\cancel{\frac{4}{3}\pi} r_1{^3}}{\cancel{\frac{4}{3}\pi} r_2^{3}}=(\frac{1}{3})^3\) \( \Rightarrow \frac{r_1^{3}}{r_2^{3}}=(\frac{1}{3})\) \( \Rightarrow (\frac{r_1}{r_2})^3=(\frac{1}{3})^3\) \( \Rightarrow \frac{r_1}{r_2}=\frac{1}{3}\).Agora, como a área a superfície de uma bola é dada por \(S=4 \pi r^2\) então a razão de proporção das superfícies das duas bolas será dada por: \( \frac{S_1}{S_2}=\frac{4 \pi r_1^{2}}{4 \pi r_2^{2}}\) \( =\frac{\cancel{4 \pi } r_1^{2}}{\cancel{4 \pi} r_2^{2}}\) \( = \frac{r_1^{2}}{r_2^{2}}\) \( = (\frac{ r_1}{r_2})^2\) \( = (\frac{1}{3})^2 \) \( =\frac{1}{9} \).
12. O conjunto das soluções da desigualidade \( \frac{x^{49}(2-x)^{51}}{(x^2-3x+2)^{100}} \ge 0 \) é:
Resolução:
Na desigualidade o segundo membro já é nulo, e o primeiro é uma fracção única. Agora vamos factorizar e achar is zeros do denominador e numerador.Assim, \( \frac{x^{49}(2-x)^{51}}{(x^2-3x+2)^{100}} \ge 0 \) \( \Rightarrow \frac{x^{49}(2-x)^{51}}{[(x-1)(x-2)]^{100 }}\ge 0 \).
\(x=0\), \(2-x=0\) \(\Rightarrow x=2\), \(x-1=0\) \(\Rightarrow x=1\) e \(x-2=0\) \(\Rightarrow x=2\).
Depois elaboramos a tabela de variação de sinais.
\(\begin{array}{|c|c|c|c|c|c|c|c|}
\hline
x & ]-\infty; 0[ & 0 & ]0;1[ & 1 & ]1;2[ & 2 & ]2;+\infty[\\
\hline
x^{49} & - & 0 & + & 1 & + & 2^{49} & +\\
\hline
(2-x)^{51} & + & 2^{51} & + & 1 & + & 0 & -\\
\hline
(x-1)^{100} & + & 1 & + & 0 & + & 1 & +\\
\hline
(x-2)^{100} & + & 2^{100} & + & 1 & + & 0 & +\\
\hline
\frac{x^{49}(2-x)^{51}}{(x^2-3x+2)^2} & - & 0 & + & \nexists & + & \nexists & -\\
\hline
\end{array}\)
Entretanto, \( x \in [0;1[ \cup ]1;2[ \).
13. Numa turma, 12 alunos são meninas. A proporção de meninas e rapazes é \(2:3\). O número de alunos é:
Resolução:
Seja \(x\) o número de alunos que são meninas e \(y\) o número dos alunos que são rapazes. Assim, \(x=12\) e \(y=?\).Agora, como a razão de proporção de meninas e rapazes é \(2:3\), então \( \frac{x}{y} = \frac{2}{3} \) \( \Rightarrow \frac{12}{y} = \frac{2}{3} \), e pela regra de três simples teremos \( y \cdot 2 = 12 \cdot 3 \) \( \Rightarrow y = 18 \).
Entretanto, o número de alunos é \(x+y =12+18 =30 \).
14. Sendo a função \(y=\frac{2}{x\sqrt{2-x}}\), então o seu domínio é:
Resolução:
Visto que trata-se de uma função Cuba expressão é irracional fraccionária, então o denominador deve ser diferente de zero e o radicando deve ser positivo.Assim, \(x \sqrt{2-x} \ne 0 \wedge 2-x \gt 0 \) \( \Rightarrow x \ne 0 \vee 2-x \ne 0 \wedge x\lt 2\) \( \Rightarrow x \ne 0 \vee x \ne 2 \wedge x \lt 2 \)
Entretanto, \( x \in ]-\infty; 2[ -\{0;2\} \) \( = ]-\infty; 0[ \cup ]0;2[ \).
15. A inequação \(\frac{x-1}{(2x+4)(3-x)} \ge 0\) tem solução:
Resolução:
Como sempre, para resolver uma inequação devemos garantir que o segundo membro seja zero. Como a inequação nos é dada uma inequação nula no segundo membro, vamos para o passo seguinte, determinar os zeros do denominador e numerador.Assim, \(x-1 = 0 \wedge 2x+4=0 \wedge 3-x = 0 \) \( \Rightarrow \) \(x=1 \wedge x=-2 \wedge x=3 \).
Em seguida elaborar-se a tabela de variação de sinais de modo a encontrarmos os intervais da solução da inequação.
\(\begin{array}{|c|c|c|c|c|c|c|c|}
\hline
x & ]-\infty; -2[ & -2 & ]-2;1[ & 1 & ]1;3[ & 3 & ]3;+\infty[\\
\hline
x-1 & - & -3 & - & 0 & + & 2 & +\\
\hline
2x+4 & - & 0 & + & 6 & + & 10 & +\\
\hline
3-x & + & 5 & + & 2 & + & 0 & -\\
\hline
\frac{x-1}{(2x+4)(3-x)} & + & \nexists & - & 0 & + & \nexists & -\\
\hline
\end{array}\)
Entretanto, \( x \in ]-\infty;-2[ \cup [1;3[ \).
16. Determine o comprimento da linha poligonal \(ABCD\) na figura sabendo que cada quadrado da rede mede de lado \(1 cm\).
Resolução:
Primeiro vamos fazer uma escala na rede de forma a nos facilitar a interpretação do problema.Analisando a figura podemos ver que é possivel criar \(3\) triângulos, onde a hipotenusa de cada um dos triângulos é um dos segmentos de recta que constituem a linha poligonal.
Vamos traçar um triângulo em que a sua hipotenusa seja o segmento de recta \(AB\).
Assim, \(|AB|=\sqrt{2^2+2^2}=2\sqrt{2}\).
Fazemos o mesmo procedimento para \(BC\) e \(CD\).
\(|BC|=\sqrt{1^2+3^2}=\sqrt{10} \).
Entretanto, o comprimento será igual a \(2\sqrt{2}+\sqrt{10}+\sqrt{5} \).
17. A solução da equação \(3^x-7^x=0\) é:
Resolução:
\(3^x-7^x=0\) \( \Rightarrow 3^x=7^x\) \(\Rightarrow \frac{3^x}{7^x}=1\) \( \Rightarrow (\frac{3}{7})^x=(\frac{3}{7})^0\) \( \Rightarrow x=0 \).18. Sejam \(a\) e \(b\) números reais positivos. Se \(\log_2{(\log_5a)}=\log_5{(\log_2b)}=0\), então \(a+b\) é igual a:
Resolução:
\( \log_2{(\log_5a)}=0 \) \( \Rightarrow \log_5a = 2^0 \) \( \Rightarrow \log_5a=1 \) \( \Rightarrow a=5^1\) \(\Rightarrow a=5 \).\( \log_5{(\log_2b)}=0 \) \( \Rightarrow \log_2b = 5^0 \) \( \Rightarrow \log_2b=1 \) \( \Rightarrow b=2^1\) \(\Rightarrow b=2 \).
Daí que \( a+b=5+2=7\).
19. Numa progressão aritmética de \(21\) termos e razão \(7\), a soma do termo do meio e do seu antecedente é igual ao último termo. Então o último termo é:
Resolução:
Seja \(N\) um número impar de termos de uma progressão artimética, então a ordem do termo médio será dada por: \( n=\frac{N+1}{2}\) \(\Rightarrow n=\frac{21+1}{2} = 11\).Então, \(a_{11}\) é o termo médio e \(a_{10}\) é o seu antecedente.
Assim, \(a_{11}+a_{10} = a_{21} \) \(\Rightarrow a_1+10d + a_1+9d=a_1+20d\) \(2a_1+10\cdot 7 + 9\cdot 7= a_1 + 20 \cdot 7\) \(\Rightarrow 2a_1-a_1 = 20 \cdot 7 - 19 \cdot 7 \) \(\Rightarrow a_1=7\).
Entretanto, \( a_{21}=a_1+20d=7+20 \cdot 7=147\).
Qualquer duvida ou sugestão, DEIXE O SEU COMENTARIO.
Obrigado!



Gostei
ResponderEliminar