Matemática anima: Identidades Trigonométricas
Oi pessoal. As identidades trigonométricas nunca desaparecem.
Sempre. Se você precisa fazer qualquer coisa na matemática, certamente as identidades trigonométricas vão estar presentes em algum ponto. É tão importante aprender a manipula-las corretamente! Existem various casos muitos diferentes, então eu não poderia possivelmente lista e ensinar para si todos eles de uma única vez. Vou mostrar-lhe aqueles que aparecem mais frequentemente nos exames extraordinários, exames finais da 10ª e 12ª Classes, assim como nos exames de admissão. Eu só vou mostrar a vocês como manipuar aquelas identidades trigonométricas que são mais úteis e frequentes.
Assim, trigonometria não é apenas sobre triângulos. É sobre a relação entre os ângulos e os comprimentos dos lados.
Descrevemos essas relações usando funções trigonométricas. Há seis delas, e você deve se sentir confortável com todos elas mas principalmente com as quadro que são mais usadas. Elas aparecem em derivadas, integrais, e podem ser usadas para simplificar expressões ou até mesmo as respostas, e elas podem ser aplicadas de muitas maneiras.
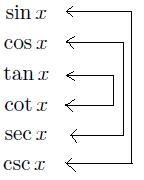
Estas são bastante fáceis de lembrar, pois há uma simetria sobre eles. Aqui está o meu truque: Listar as 6 funções trigonométricas. Os dois do lado de fora ficam juntos, o segundo e o penúltimo ficam juntos, e os dois do meio ficam juntos. Deixe-me mostrar como eu imagino. Escreva-os verticalmente, e desenhe linhas para combiná-los. Isto irá dizer-lhe que o \(seno\) fica com \(cosecante\), \(cosseno \) vai ficar com \(secante\), e \(tangente \) vai com \(cotangente \).
Entendeu? Se está sempre com dúvida, basta escrever isso muito rapidamente.
Nunca vai ficar errar!
Estas duas identidades são extremamente importantes, e não muito difícil de lembrar. Mantenha-as em mente, porque você definitivamente vai precisar delas.
\[ \mathrm{sen}2x=2\mathrm{sen}x•\cos x \]
Estas duas são também muito importantes de se saber. A primeira surge com maior frequência e a segunda menos frequentemente. No entanto, todos elas saem nos exames muitas vezes!
Você precisa estar atento. Se você tem uma expressão com muitas funções trigonométricas diferentes dentro dela, tente pensar se ela pode ser simplificada. Siga meu método e veja o que você pode fazer. Às vezes ficará surpreso, e as coisas podem ser simplificadas drasticamente.
Esse deve ser o seu primeiro passo o tempo todo. Se você poder flagrantemente ver uma das identidades, aplica imediatamente e simplifica. Não pule sobre eles apenas para seguir meu processo.
Use a factorização ou volte a usar as identidades para simplificar a expressão.
Converta de volta para tangentes e cotangentes quando necessário, e outras coisas como isso. Livra-se de tantas frações sempre que possível. E só depois de fazermos todas as operações possíveis é que podemos dizer que encontrarmos a resposta final.
Aqui estão dois exemplos de expressões complexas, que vou simplificar o máximo possível. Há muitas outros casos possíveis, mas eu não posso mostrar todos os tipos de exemplos. Existem muitos. Seguindo este processo com ajuda você simplifica praticamente qualquer expressão trigonométrica, o que é necessário em muitas situações!
Exemplo 1. (Questão 9 do Exame de Matemática 12ª Classe 2ª Época -2014)
A que é igual \( \frac{\mathrm{tg}x +1}{\cos x + \mathrm{sen}x} \)?
Imediatamente, eu não vejo nenhuma simplificação fácil. Então, eu converto tudo para o seno e cosseno.
\( \frac{\frac{\mathrm{sen}x}{\cos x} +1}{\cos x + \mathrm{sen}x} \)
Agora, vejo que o numerador pode ser transformado em apenas um único termo atraves de mmc.
\( \frac{\frac{\mathrm{sen}x +\cos x}{\cos x}}{\cos x + \mathrm{sen}x} \)
Agora, como trata-se de uma fracção de uma fracção então podemos inverter o denominador e passar a multiplicar porque quando você divide por uma fração, é o mesmo que multiplicar pelo seu recíproco.
\( \frac{\mathrm{sen}x+\cos x}{\cos x}•\frac{1}{\cos x + \mathrm{sen}x} \)
Então, há uma simplificação muito fácil de \(\mathrm{sen}x+\cos x\) com \(\cos x + \mathrm{sen}x\) pois são iguais e estão a dividir-se entre si.
\( \frac{\cancel{\mathrm{sen}x +\cos x}}{\cos x\cancel{(\cos x + \mathrm{sen}x)}} \)
Entretanto, ficamos com \(\frac{1}{\cos x}\). E já não é preciso fazer mais nada.
Exemplo 2. (Questão 9 do Exame de Matemática 12ª Classe 2ª Época -2014)
A que é igual \(\frac{1-\mathrm{sen}^2x}{\mathrm{sen}x•\cos x} \)?
Nesta expressão, algo vem logo na minha mente. Eu estou sempre à procura de ver um seno ao quadrado ou um cos ao quadrado proximo um do outro ou proximo do número um. Neste caso temos seno ao quadrado e um. Como eles estão sendo subtraidos juntos, você pode simplifica-los usando uma identidade trigonométrica. Como seno ao quadrado mais cosseno ao quadrado é igual a um. Então podemos substituir no lugar de um.
\(\frac{\mathrm{sen}^2x +\cos^2x-\mathrm{sen}^2x}{\mathrm{sen}x•\cos x} \)
Em seguida vamos simplificar os termos semelhantes.
\(\frac{\cancel{\mathrm{sen}^2x}+\cos^2x-\cancel{\mathrm{sen}^x}}{\mathrm{sen}x•\cos x}\) \(=\frac{\cos^2x}{\mathrm{sen}x•\cos x} \)
Agora pode ver que no numerador temos cosseno de \(x\) e no denominador tambem, então vamos simplificar porque eles estão se dividido entre si vai dar um.
\(\frac{\cos x • \cos x}{\mathrm{sen}x•\cos x} \) \(=\frac{\cos x}{\mathrm{sen}x} \) \(=\mathrm{cotg}x\)
Pode ter a certeza que aprendeu algo que sem duvida lhe vai ser muito útil.
Espero que você possa me seguir! Espero que isso tenha lhe ajudado! Como sempre, deixe um comentário abaixo ou envie um e-mail para mim (veja no meu perfil) com quaisquer perguntas ou comentários.
Sempre. Se você precisa fazer qualquer coisa na matemática, certamente as identidades trigonométricas vão estar presentes em algum ponto. É tão importante aprender a manipula-las corretamente! Existem various casos muitos diferentes, então eu não poderia possivelmente lista e ensinar para si todos eles de uma única vez. Vou mostrar-lhe aqueles que aparecem mais frequentemente nos exames extraordinários, exames finais da 10ª e 12ª Classes, assim como nos exames de admissão. Eu só vou mostrar a vocês como manipuar aquelas identidades trigonométricas que são mais úteis e frequentes.
Assim, trigonometria não é apenas sobre triângulos. É sobre a relação entre os ângulos e os comprimentos dos lados.
Descrevemos essas relações usando funções trigonométricas. Há seis delas, e você deve se sentir confortável com todos elas mas principalmente com as quadro que são mais usadas. Elas aparecem em derivadas, integrais, e podem ser usadas para simplificar expressões ou até mesmo as respostas, e elas podem ser aplicadas de muitas maneiras.
Identidades Recíprocas
\(\begin{align} &\mathrm{sen}x=\frac{1}{\mathrm{cosec} x} \quad & \mathrm{cosec}x=\frac{1}{\mathrm{sen}x}\\ &\cos x=\frac{1}{\mathrm{sec}x} \quad & \sec x=\frac{1}{\cos x}\\ &\mathrm{tg}x=\frac{1}{\mathrm{cotg}x} \quad & \mathrm{cotg }x=\frac{1}{\mathrm{tg}x} \end{align}\)Estas são bastante fáceis de lembrar, pois há uma simetria sobre eles. Aqui está o meu truque: Listar as 6 funções trigonométricas. Os dois do lado de fora ficam juntos, o segundo e o penúltimo ficam juntos, e os dois do meio ficam juntos. Deixe-me mostrar como eu imagino. Escreva-os verticalmente, e desenhe linhas para combiná-los. Isto irá dizer-lhe que o \(seno\) fica com \(cosecante\), \(cosseno \) vai ficar com \(secante\), e \(tangente \) vai com \(cotangente \).
Entendeu? Se está sempre com dúvida, basta escrever isso muito rapidamente.
Nunca vai ficar errar!
Tangente e Cotangente
\[ \mathrm{tg}x=\frac{\mathrm{sen}x}{\cos x} \quad \mathrm{cotg}x=\frac{\cos x}{\mathrm{sen}x} \]Estas duas identidades são extremamente importantes, e não muito difícil de lembrar. Mantenha-as em mente, porque você definitivamente vai precisar delas.
Outras Identidades Importantes
\[ \mathrm{sen}^2x+\cos^2x=1\]\[ \mathrm{sen}2x=2\mathrm{sen}x•\cos x \]
Estas duas são também muito importantes de se saber. A primeira surge com maior frequência e a segunda menos frequentemente. No entanto, todos elas saem nos exames muitas vezes!
Como elas são usadas?
Eu vou ensinar-lhe a técnica que eu uso para simplificar funções trigonométricas complexas. Você vê muitas vezes ao longo da disciplina de matemática. Eu não vou mostrar-lhe problemas específicos, apenas grandes expressões que vou simplificar.Você precisa estar atento. Se você tem uma expressão com muitas funções trigonométricas diferentes dentro dela, tente pensar se ela pode ser simplificada. Siga meu método e veja o que você pode fazer. Às vezes ficará surpreso, e as coisas podem ser simplificadas drasticamente.
1° Passo: Procure simplificações óbvias.
Esse deve ser o seu primeiro passo o tempo todo. Se você poder flagrantemente ver uma das identidades, aplica imediatamente e simplifica. Não pule sobre eles apenas para seguir meu processo.2° Passo: Converta tudo para o seno e cosseno.
Faça isso usando identidades recíprocas e identidades tangentes e cotangentes. Agora, você pode ver se da para combinar como termos ou eliminar frações.
3° Passo: Agora, faça todo o cancelamento possível!
Use a factorização ou volte a usar as identidades para simplificar a expressão.4° Passo: O último passo é escrever todas as expressões mais adequadas.
Por exemplo, se você tem um seno no numerador e um cosseno no denominador, podemos e devemos, transformar essa razão em uma tangente.Converta de volta para tangentes e cotangentes quando necessário, e outras coisas como isso. Livra-se de tantas frações sempre que possível. E só depois de fazermos todas as operações possíveis é que podemos dizer que encontrarmos a resposta final.
Aqui estão dois exemplos de expressões complexas, que vou simplificar o máximo possível. Há muitas outros casos possíveis, mas eu não posso mostrar todos os tipos de exemplos. Existem muitos. Seguindo este processo com ajuda você simplifica praticamente qualquer expressão trigonométrica, o que é necessário em muitas situações!
Exemplo 1. (Questão 9 do Exame de Matemática 12ª Classe 2ª Época -2014)
A que é igual \( \frac{\mathrm{tg}x +1}{\cos x + \mathrm{sen}x} \)?
Imediatamente, eu não vejo nenhuma simplificação fácil. Então, eu converto tudo para o seno e cosseno.
\( \frac{\frac{\mathrm{sen}x}{\cos x} +1}{\cos x + \mathrm{sen}x} \)
Agora, vejo que o numerador pode ser transformado em apenas um único termo atraves de mmc.
\( \frac{\frac{\mathrm{sen}x +\cos x}{\cos x}}{\cos x + \mathrm{sen}x} \)
Agora, como trata-se de uma fracção de uma fracção então podemos inverter o denominador e passar a multiplicar porque quando você divide por uma fração, é o mesmo que multiplicar pelo seu recíproco.
\( \frac{\mathrm{sen}x+\cos x}{\cos x}•\frac{1}{\cos x + \mathrm{sen}x} \)
Então, há uma simplificação muito fácil de \(\mathrm{sen}x+\cos x\) com \(\cos x + \mathrm{sen}x\) pois são iguais e estão a dividir-se entre si.
\( \frac{\cancel{\mathrm{sen}x +\cos x}}{\cos x\cancel{(\cos x + \mathrm{sen}x)}} \)
Entretanto, ficamos com \(\frac{1}{\cos x}\). E já não é preciso fazer mais nada.
Exemplo 2. (Questão 9 do Exame de Matemática 12ª Classe 2ª Época -2014)
A que é igual \(\frac{1-\mathrm{sen}^2x}{\mathrm{sen}x•\cos x} \)?
Nesta expressão, algo vem logo na minha mente. Eu estou sempre à procura de ver um seno ao quadrado ou um cos ao quadrado proximo um do outro ou proximo do número um. Neste caso temos seno ao quadrado e um. Como eles estão sendo subtraidos juntos, você pode simplifica-los usando uma identidade trigonométrica. Como seno ao quadrado mais cosseno ao quadrado é igual a um. Então podemos substituir no lugar de um.
\(\frac{\mathrm{sen}^2x +\cos^2x-\mathrm{sen}^2x}{\mathrm{sen}x•\cos x} \)
Em seguida vamos simplificar os termos semelhantes.
\(\frac{\cancel{\mathrm{sen}^2x}+\cos^2x-\cancel{\mathrm{sen}^x}}{\mathrm{sen}x•\cos x}\) \(=\frac{\cos^2x}{\mathrm{sen}x•\cos x} \)
Agora pode ver que no numerador temos cosseno de \(x\) e no denominador tambem, então vamos simplificar porque eles estão se dividido entre si vai dar um.
\(\frac{\cos x • \cos x}{\mathrm{sen}x•\cos x} \) \(=\frac{\cos x}{\mathrm{sen}x} \) \(=\mathrm{cotg}x\)
Pode ter a certeza que aprendeu algo que sem duvida lhe vai ser muito útil.
Espero que você possa me seguir! Espero que isso tenha lhe ajudado! Como sempre, deixe um comentário abaixo ou envie um e-mail para mim (veja no meu perfil) com quaisquer perguntas ou comentários.

Comentários
Enviar um comentário