Resolução 40-49 Exame UEM-2013
Ir para:1-10 | 11-19 | 20-29 | 30-39 | 50-57
E também podemos verificar claramente que o vértice da parabola esta deslocado mais para a direita em relação ao eixo das ordenadas, entretanto o valor do coeficiente \(b\) é negativo, isto é, \(b\lt 0\).
Do mesmo modo o vértice da parabola está deslocado mais para baixo em relação ao eixo das abcissas, então o valor do coeficiente \(c\) é negativo, isto é, \(c \lt 0 \).
Entretanto, \( a \lt 0\), \( b \lt 0 \) e \( c \lt 0 \).
\( f'(x)=(x^2+2px-3)'\) \(=2x+2p\) \(\Rightarrow f'(1)=2\cdot 1+2p\) \(=2+2p\).
Como \(x=1\) é um extremo mínimo da função, então \(2+2p=0\) \(\Rightarrow p=-\frac{2}{2}\) \(\Rightarrow p=-1\).
Entretanto, \( f(2)=2^2+2\cdot (-1)\cdot 2-3\) \(=4-4-3\) \(=-3\).
Trando-se de uma função linear modular, vamos começar por esboçar o gráfico de \(y=x\).
Em seguida vamos traçar o gráfico de \(y=|x|\).
Podemos ver que o gráfico esta virada para baixo, então teremos \(y=-|x|\).
Depois o gráfico é afastado uma unidade para a esquerda, assim, \(y=-|x+1|\).
E por último o gráfico é afastado uma unidade para cima, daí que: \(y=-|x+1|+1=1-|x+1|\).
Assim, \(a^{-1}+b^{-1}\) \(=\frac{1}{a}+\frac{1}{b}\) \(=\frac{a+b}{a\cdot b}\).
Agora, podemos verificar que o numerador da fracção \(\frac{a+b}{ab}\) é representado pela soma das raizes da equação. E o denominador é representado pelo produto das raizes da dada equação.
Daí que \( \frac{a+b}{ab}= \frac{S}{P}\) \(=\frac{-\frac{b}{a}}{\frac{c}{a}}\) \(=\frac{-\frac{-5}{1}}{\frac{-1}{1}}\) \(=\frac{5}{-1}\) \(=-5\).
\(x^{-1} \lt 0,25\) \(\Rightarrow \frac{1}{x} \lt \frac{1}{4}\) \(\Rightarrow \frac{1}{x}-\frac{1}{4} \lt 0\) \(\Rightarrow \frac{4-x}{4} \lt 0\).
De seguida achamos os zeros para o numerador e para o denominador.
\(4-x=0 \Rightarrow x=0\) e \(4x=0 \Rightarrow x=0\).
Por fim elaboramos a tabela de variação de sinais para encontrarmos os intervais que satisfazem a desigualidade.
\(\begin{array}{|c|c|c|c|c|c|}
\hline
x & ]-\infty; 0[ & 0 & ]0;4[ & 4 & ]4;+\infty[\\
\hline
4-x & + & 4 & + & 0 & - \\
\hline
x & - & 0 & + & 4 & + \\
\hline
\frac{4-x}{x} & - & \nexists & + & 0 & -\\
\hline
\end{array}\)
Entretanto, \( x \in ]-\infty;0[\cup]4;+\infty[\).
Assim, visto que o gráfico de \(f\) tem pelo menos um ponto em comum com a recta \(y=a\) e \( a \in I\!\!R\), então o contradomínio de \(f\) conscide com o conjunto Imagem.
Entretanto, \(f\) é sobrejectiva.
Assim, \((\mathrm{sen}x+\cos x)^2\) \(=\mathrm{sen^2}x+2\cos x \mathrm{sen}x + \cos^2x \) \(=\mathrm{sen^2}x+\cos^2x \mathrm{sen}2x \) \(=1+ \mathrm{sen}2x \).
Agora, sabendo que o contradomínio de \(\mathrm{sen}2x\) é \(y \in [-1;1]\), então o contradomínio de \(1+\mathrm{sen}2x\) é \( y \in [-1+1;1+2]\) \(\Rightarrow y \in [0;2]\).
Entretanto, o contradomínio a expressão dada é \( y \in [0;2]\).
\(B)\) É falsa. Porque o contradomínio da função tangente \(y:y\in I\!\!R\).
\(C)\) É verdadeira. Porque a base do logaritmo é \(10\).
\(D)\) É verdadeira. Pois qualquer número positivo elevado a um outro qualquer número seja este positivo, negativo ou zero, é sempre um número positivo, isto é, um número que pertence ao conjunto \( ]0;+\infty[\).
\(E)\) É verdadeira. Porque podemos facilmente verificar apartir do gráfico da função cosseno que esta afirmação é verdadeira.
Assim, vamos verificar se a sequência é geometrica out não.
\(q=\frac{a_{k+1}}{a_k}\) \(=\frac{-(0,5)^{-(k+1)}}{-(0,5)^{-k}}\) \(=\frac{0,5^{-k-1}}{0,5^{-k}}\) \(=0,5^{-k-1+k}\) \(=0,5^{-1}\) \(=(\frac{1}{2})^-1\) \(=2\).
Como \(2\) é uma constante então a sequência é geometrica.
Agora devemos verificar se a sequência é crescente ou decrescente.
Para tal, podemos determinar as primeiros \(3\) termos e analisar o seu comportamento.
\(a_1=-(0,5)^{-1}\) \(=-(\frac{1}{2})^{-1}\) \(=-2\).
\(a_2=-(0,5)^{-2}\) \(=-(\frac{1}{2})^{-2}\) \(=-4\).
\(a_3=-(0,5)^{-3}\) \(=-(\frac{1}{2})^{-3}\) \(=-8\).
Como \(a_1\gt a_2\gt a_3 ...\), podemos concluir que a sequência é decrescente.
Entretanto, a sequência é geometrica decrescente.
Ir para:1-10 | 11-19 | 20-29 | 30-39 | 50-57
40. À direita está representado o gráfico de uma função quadrática \( y=ax^2+bx+c\), cujos parâmetros satisfazem as desigualidades:
Resolução:
Como a parabola está virada para baixo então é claro que o valor do coeficiente \(a\) é negativo, isto é, \(a \lt 0\).E também podemos verificar claramente que o vértice da parabola esta deslocado mais para a direita em relação ao eixo das ordenadas, entretanto o valor do coeficiente \(b\) é negativo, isto é, \(b\lt 0\).
Do mesmo modo o vértice da parabola está deslocado mais para baixo em relação ao eixo das abcissas, então o valor do coeficiente \(c\) é negativo, isto é, \(c \lt 0 \).
Entretanto, \( a \lt 0\), \( b \lt 0 \) e \( c \lt 0 \).
41. Sabendo que a função quadrática \(f(x)=x^2+2px-3\) atinge o seu mínimo no ponto \(x=1\), calcule a ordenada do ponto do gráfico de \(f\) com abcissa \(x=2\).
Resolução:
Como a primeira derivada de uma função pode nos ajudar a achar os extremos da função, então vamos determinar a derivada da função para a abcissa \( x=1\).\( f'(x)=(x^2+2px-3)'\) \(=2x+2p\) \(\Rightarrow f'(1)=2\cdot 1+2p\) \(=2+2p\).
Como \(x=1\) é um extremo mínimo da função, então \(2+2p=0\) \(\Rightarrow p=-\frac{2}{2}\) \(\Rightarrow p=-1\).
Entretanto, \( f(2)=2^2+2\cdot (-1)\cdot 2-3\) \(=4-4-3\) \(=-3\).
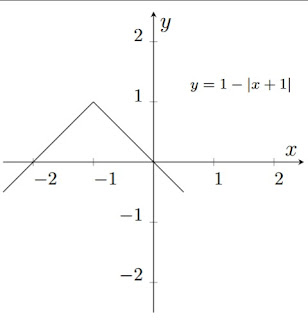
42. O gráfico ao lado representa a função
Resolução:
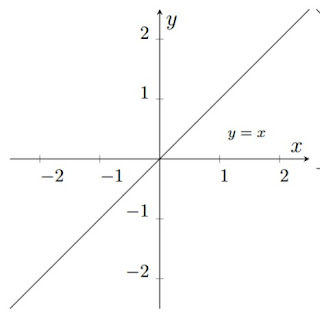
Para encontrarmos a função à que o gráfico representa, vamos usar o metodo de transladação.Trando-se de uma função linear modular, vamos começar por esboçar o gráfico de \(y=x\).
Em seguida vamos traçar o gráfico de \(y=|x|\).
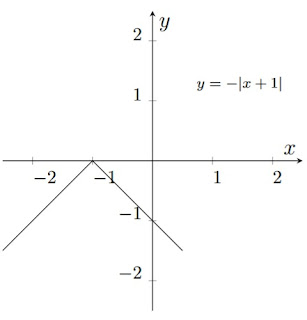
Podemos ver que o gráfico esta virada para baixo, então teremos \(y=-|x|\).
Depois o gráfico é afastado uma unidade para a esquerda, assim, \(y=-|x+1|\).
E por último o gráfico é afastado uma unidade para cima, daí que: \(y=-|x+1|+1=1-|x+1|\).
43. Se \(a\) e \(b\) são raizes diferentes da equação \(x^2-5x-2=0\), então a grandeza \(a^{-1} + b^{-1} \) é igual a:
Resolução:
Primeiro começamos por transformar \(a^{-1}+b^{-1}\).Assim, \(a^{-1}+b^{-1}\) \(=\frac{1}{a}+\frac{1}{b}\) \(=\frac{a+b}{a\cdot b}\).
Agora, podemos verificar que o numerador da fracção \(\frac{a+b}{ab}\) é representado pela soma das raizes da equação. E o denominador é representado pelo produto das raizes da dada equação.
Daí que \( \frac{a+b}{ab}= \frac{S}{P}\) \(=\frac{-\frac{b}{a}}{\frac{c}{a}}\) \(=\frac{-\frac{-5}{1}}{\frac{-1}{1}}\) \(=\frac{5}{-1}\) \(=-5\).
44. Todas as soluções da inequação \( x^{-1} \lt 0,25 \) formam o conjunto:
Resolução:
Sempre que queros resolver uma inequação devemos anular o segundo membro (o segundo membro deve ser zero).\(x^{-1} \lt 0,25\) \(\Rightarrow \frac{1}{x} \lt \frac{1}{4}\) \(\Rightarrow \frac{1}{x}-\frac{1}{4} \lt 0\) \(\Rightarrow \frac{4-x}{4} \lt 0\).
De seguida achamos os zeros para o numerador e para o denominador.
\(4-x=0 \Rightarrow x=0\) e \(4x=0 \Rightarrow x=0\).
Por fim elaboramos a tabela de variação de sinais para encontrarmos os intervais que satisfazem a desigualidade.
\(\begin{array}{|c|c|c|c|c|c|}
\hline
x & ]-\infty; 0[ & 0 & ]0;4[ & 4 & ]4;+\infty[\\
\hline
4-x & + & 4 & + & 0 & - \\
\hline
x & - & 0 & + & 4 & + \\
\hline
\frac{4-x}{x} & - & \nexists & + & 0 & -\\
\hline
\end{array}\)
Entretanto, \( x \in ]-\infty;0[\cup]4;+\infty[\).
45. Seja dada uma função \(y=f(x)\) definida em \( I\!\!R\) que satisfaz à seguinte condição: para todo \( a \in I\!\!R \) a recta horizontal \(y=a\) e o gráfico da função \(f\) têm pelo menos um ponto em comum. É correcto dizer que a função \(f\) é:
Resolução:
Como \(a \in I\!\!R\), então \( y \in I\!\!R\).Assim, visto que o gráfico de \(f\) tem pelo menos um ponto em comum com a recta \(y=a\) e \( a \in I\!\!R\), então o contradomínio de \(f\) conscide com o conjunto Imagem.
Entretanto, \(f\) é sobrejectiva.
46. O domínio de definição da função \( f(x)=\lg{(\lg{x})} \) é:
Resolução:
Tratando-se de uma função logaritmica temos que o logaritmando deve sempre ser positivo, daí que \(\lg x \gt 0 \wedge x\gt 0\) \( \Rightarrow \lg x \gt \lg 1 \wedge x \gt 0 \) \( \Rightarrow x \gt 1 \wedge x \gt 0\) \( \Rightarrow x\in ]1;+\infty[ \cup ]0;+\infty[ \) \( \Rightarrow x \in ]1; +\infty[ \).47. O conjunto imagem (o contradomínio) da função \(f(x)=(\mathrm{sen}x+\cos x)^2\) é:
Resolução:
Em primeiro lugar vamos desenvolver a expressão \((\mathrm{sen}x+\cos x)^2\).Assim, \((\mathrm{sen}x+\cos x)^2\) \(=\mathrm{sen^2}x+2\cos x \mathrm{sen}x + \cos^2x \) \(=\mathrm{sen^2}x+\cos^2x \mathrm{sen}2x \) \(=1+ \mathrm{sen}2x \).
Agora, sabendo que o contradomínio de \(\mathrm{sen}2x\) é \(y \in [-1;1]\), então o contradomínio de \(1+\mathrm{sen}2x\) é \( y \in [-1+1;1+2]\) \(\Rightarrow y \in [0;2]\).
Entretanto, o contradomínio a expressão dada é \( y \in [0;2]\).
48. Escolha a afirmação falsa:
Resolução:
\(A)\) É verdadeira. Porque para qualquer \(x \in I\!\!R\), \(\mathrm{sen}x\) sempre tem sentido.\(B)\) É falsa. Porque o contradomínio da função tangente \(y:y\in I\!\!R\).
\(C)\) É verdadeira. Porque a base do logaritmo é \(10\).
\(D)\) É verdadeira. Pois qualquer número positivo elevado a um outro qualquer número seja este positivo, negativo ou zero, é sempre um número positivo, isto é, um número que pertence ao conjunto \( ]0;+\infty[\).
\(E)\) É verdadeira. Porque podemos facilmente verificar apartir do gráfico da função cosseno que esta afirmação é verdadeira.
49. A sequência \( a_1; a_2; a_3; ... \) em que \( a_k=-(0,5)^{-k}\), (\( k \in I\!\!R \) é:
Resolução:
Tratando-se de uma potência, podemos logo suspeitar que a sequência seja geometrica.Assim, vamos verificar se a sequência é geometrica out não.
\(q=\frac{a_{k+1}}{a_k}\) \(=\frac{-(0,5)^{-(k+1)}}{-(0,5)^{-k}}\) \(=\frac{0,5^{-k-1}}{0,5^{-k}}\) \(=0,5^{-k-1+k}\) \(=0,5^{-1}\) \(=(\frac{1}{2})^-1\) \(=2\).
Como \(2\) é uma constante então a sequência é geometrica.
Agora devemos verificar se a sequência é crescente ou decrescente.
Para tal, podemos determinar as primeiros \(3\) termos e analisar o seu comportamento.
\(a_1=-(0,5)^{-1}\) \(=-(\frac{1}{2})^{-1}\) \(=-2\).
\(a_2=-(0,5)^{-2}\) \(=-(\frac{1}{2})^{-2}\) \(=-4\).
\(a_3=-(0,5)^{-3}\) \(=-(\frac{1}{2})^{-3}\) \(=-8\).
Como \(a_1\gt a_2\gt a_3 ...\), podemos concluir que a sequência é decrescente.
Entretanto, a sequência é geometrica decrescente.
Ir para:1-10 | 11-19 | 20-29 | 30-39 | 50-57



Comentários
Enviar um comentário