Exame Resolvido UEM - 2011 - 21 a 30
Solução:
Sabendo que o contradominio de \(y=\mathrm{sen}x\) é \(y \in [-1;1]\), então podemos afirmar que a equação \(\mathrm{sen}x=\frac{4}{3} \) não tem solução porque \( \frac{4}{3} \notin [-1;1] \).
Solução:
Tratando-se de uma função do tipo \(f(x)=\frac{ax+b}{cx+d}\), podemos determinar as assimptotas com base nas seguintes formulas:
A.V.: \(x=\frac{-d}{c}\) \(=\frac{-(-1)}{1}\) \(=1\).
A.H.: \(y=\frac{a}{c}\) \(\frac{1}{1}\) \(=1\).
Entretanto, a alternativa correcta é \(A\), pois o gráfico desta alternativa tem como assimptota vertical \(x=1\) e assimptota horizontal \(y=1\).
Solução:
O contradomínio de uma função é igual ao domínio da inversa dessa função.
Sendo assim, vamos determinar a inversa da função dada.
\(x=\dfrac{1}{1-y^{-1}}+2\) \(\Rightarrow x-2=\dfrac{1}{1-y^{-1}}\) \(\Rightarrow 1-y^{-1}=\dfrac{1}{x-2}\) \(\Rightarrow 1-\dfrac{1}{x-2}=y^{-1}\) \(\Rightarrow y^{-1}=1-\dfrac{1}{x-2}\).
Agora vamos encontrar o domínio da inversa de \(y\).
\(x-2\ne 0\) \(\Rightarrow x\ne 2\).
Entretanto o ntradomínio de uma função \(y\) é \(x\in I\!\!R / \{2\}\).
Solução:
A diagonal de um rectângulo é a hipotenusa do triângulo formado por dois lados consecutivos. Logos esses dois lados consecutivos são os catetos desse triângulo.
Assim, podemos concluir que: \(c_1+c_2=14\) e \( h=10 \).
Pelo teorema de pitagoras temos que \(c_1^2+c_2^2=h^2\) \( \Rightarrow c_1^2+c_2^2 +2c_1c_2-2c_1c_2=h^2 \) \( \Rightarrow (c_1+c_2)^2-2c_1c_2=h^2 \) \( \Rightarrow 14^2-2c_1c_2=10^2 \) \( \Rightarrow 196-2c_1c_2=100 \) \( \Rightarrow -2c_1c_2=100-196 \) \( \Rightarrow c_1c_2=\frac{-96}{-2} \) \( \Rightarrow c_1c_2=48 \).
Entretanto a área de um rectângulo, em \(cm^2\), é 48. Porque a área de um rectângulo é dada pelo produto de dois lados consecutivos do mesmo.
25. Num curso de iniciação à informática, a distribuição das idades dos alunos, segundo o sexo, é dada pelo gráfico seguinte. Com base nos dados do gráfico, pode-se afirmar que:
Solução:
Vamos avaliar cada afirmação de modo a encontrarmos a que é correcta:
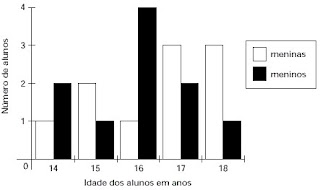
A. O número de meninas com, no máximo, 16 anos é maior que o número de meninos nesse mesmo intervalo de idades.
O número de meninas com, no máximo, 16 anos é igual a \(1+2+1\) \(=4\).
O número de meninos com, no máximo, 16 anos é igual a \(2+1+4\) \(=7\).
Logo esta afirmação é incorrecta.
B. O número total de alunos é 19.
O número total de alunos é igual a \(1+2+2+1+1+4+3+2+3+1\) \(=20\).
Logo esta afirmação tambem é incorrecta.
C. A média de idade das meninas é 15 anos.
A média de idade das meninas é igual a \( \frac{1\cdot 14+ 2\cdot 15 + 1\cdot 16+3\cdot 17+3\cdot 18}{1+2+1+3+3} \) \(=\frac{14+30+16+51+54}{10} \) \(=\frac{165}{10} \) \(=16,5\).
Esta afirmação tambem é incorrecta.
D. O número de meninos é igual ao número de meninas.
O número de meninos é igual a \(2+1+4+2+1\) \(=10\).
O número de meninas é igual a \(1+2+1+3+3\) \(=10\).
Logo esta é a afirmação correcta.
E. O número de meninos com idade superior a 15 anos é maior que o número de meninas nesse mesmo intervalo de idades.
O número de meninos com idade superior a 15 anos é igual a \(4+2+1\) \(=7\).
O número de meninas com idade superior a 15 anos é igual a \(1+3+3\) \(=7\).
Logo esta afirmação é incorrecta.
Solução:
Os extremos de uma função são determinados atraves da sua primeira derivada.
Assim, vamos determinar a primeira derivada de \(f(x)\).
\(f'(x)= (x^3-1)'\) \(=2x^2-0\) \(=2x^2\).
Agora ao analisar a primeira derivada da função dada, conseguimos notar que ele é não negativa em todo o seu dominio. Logo isso significa que a função \(f(x)\) é crescente em todo o seu dominio.
Entretanto, \(f(x)\) não tem extremos.
Solução:
Tratando-se de uma função racional fraccionaria, então ela não tem sentido quando o denominador é igual a zero. Sendo assim, podemos concluir que \( x^2+1 \ne 0 \). Agora, como \(x^2+1\) é sempre positivo para qualquer valor real de \(x\), então \( x^2+1\) é diferente de zero para qualquer valor real de \(x\).
Entretanto, o domínio da função \(f(x)=\dfrac{x}{x^2+1}\) é \(I\!\!R\).
Solução:
\((\ln x^2)'=\frac{(x^2)'}{x^2}\) \(=\frac{2x}{x^2}\) \(=\frac{2}{x}\).
Solução:
\(\displaystyle \lim_{x\to -3}\frac{x^2-9}{x+3} = \displaystyle \lim_{x\to -3}\frac{x^2-3^2}{x+3} \) \(=\displaystyle \lim_{x\to -3}\frac{(x-3)(x+3)}{x+3} \)
\(= \displaystyle \lim_{x\to -3}{x-3} \) \(=-3-3\) \(=-6\).
Solução:
\(\displaystyle \lim_{x\to \infty}5e^{-x} = \displaystyle \lim_{x\to \infty}5e^{-\infty} \) \(= \displaystyle \lim_{x\to \infty}\frac{5}{e^{+\infty}} \) \(= \displaystyle \lim_{x\to \infty}\frac{5}{+\infty} \) \(= 0 \).
Comentários
Enviar um comentário