EXAME RESOLVIDO 11-20 - UEM-2004

11. A figura apresenta parte da representação gráfica de uma função \(f\) de domínio \(I\!\!R\). Qual das seguintes afirmações é verdadeira?

Resolução:
A analisarmos a figura podemos concluir que:
Quando \(x\) se aproxima de 3 pela esquerda (\(3^-\)), o valor de \(y\) não se aproxima de \(f(3)\). Então, \(\displaystyle \lim_{x\to 3^-}f(x)\ne f(3)\).

Quando \(x\) se aproxima de 3 pela direita (\(3^+\)), o valor de \(y\) se aproxima de \(f(3)\). Então, \(\displaystyle \lim_{x\to 3^+}f(x)= f(3)\).

12. A solução da equação \((\frac{1}{2})^x-(\frac{1}{4})^x=0\) é

Resolução:
Para resolver equações exponenciais, você precisa ter equações com expressões exponenciais comparáveis ​​em ambos os lados do sinal "igual", para que você possa comparar os expoentes e resolver. Em outras palavras, você tem que ter "(alguma base) para (algum expoente) igual (a mesma base) a (algum outro expoente)", onde você ajusta as duas potências iguais entre si e resolve a equação resultante. Assim:
\((\frac{1}{2})^x-(\frac{1}{4})^x=0\) \(\Rightarrow (\frac{1}{2})^x=(\frac{1}{4})^x\) \(\Rightarrow (\frac{1}{2})^x=(\frac{1}{2})^{2x}\)

Uma vez que as bases (\("\frac{1}{2}\)" em cada caso) são as mesmas, então a única maneira das duas expressões poderem ser iguais é se as potências também forem as mesmas. Isso é:
\(x=2x\) \(\Rightarrow 2x-x=0\) \(\Rightarrow x=0\).
Esta solução demonstra como essa classe inteira de equação é resolvida: se as bases são as mesmas, então as potências também devem ser as mesmas, para que os dois membros da equação sejam iguais entre si.
Uma vez que os expoentes devem ser os mesmos, então você pode definir as duas potências iguais entre si, e resolver a equação resultante.

13. De uma função \(h\) definida num certo domínio, sabe-se que a sua derivada \(h'\) está igualmente definida no mesmo domínio e é dada por \(h'(x)=x+3\cos{x}\). O valor de \(\displaystyle \lim_{x \to 0} \frac{h(x)-h(0)}{x}\) é:

Resolução:
A derivada de uma função \(h(x)\) é uma outra função \(h'(x)\) e é definida da seguinte forma:\[h'(x_0)=\lim_{x\to x_0}\frac{h(x)-h(x_0)}{x-x_0}\]
Assim, \(x_0=0\) e \( h'(x_0)=x_0+3\cos{x_0}\).
Entretanto, \(\lim_{x\to x_0}\frac{h(x)-h(x_0)}{x-x_0}\) \(=x_0+3\cos{x_0}\) \(=0+3\cos{0}\) \(=3\cdot 1\) \(=3\).

14. Qual é a medida do lado \(x\) sabendo que \(AC // BE\)?

Resolução:
Como \(AC\) é paralelo a \(BE\), então os triângulos \(ACD\) e \(BED\) são semelhantes.
Assim, pela regra dos triângulos semelhantes temos que:
\(\frac{x}{3+5}=\frac{4}{5}\) \(\Rightarrow x=\frac{4\cdot 8}{5}\) \(\Rightarrow x=6,4\).

15. Qual é o valor da soma algébrica \(\displaystyle sen 240° - cos 150° + tg 330°\).

Resolução:
\(240°\) está no terceiro quadrante então o \(seno\) é negativo. Assim, \(sen 240°=-sen(240°-180°)=-sen 60°\).
\(150°\) está no segundo quadrante, então o \(cosseno\) é negativo. Assim, \(\cos 150°=-\cos (180°-150°)=-\cos 30°\).
\(330°\) está no quarto quadrante, então a \(tangente\) é negativa. Assim, \(tg 330°=-tg(360°-330°)=-tg 30°\).

Depois vamos substituir os valores encontrados na dada expressão:
\(\displaystyle sen 240° - cos 150° + tg 330°\) \(=\displaystyle -sen 60° - (-cos 30°) +(- tg 30°)\) \(=\displaystyle -\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} -\frac{\sqrt{3}}{3}\) \(=\displaystyle -\frac{\sqrt{3}}{3}\).

16. No intervalo \([-\pi;2\pi ]\), a solução da inequação \(\displaystyle -\frac{1}{2}\le sen x\) é:

Resolução:
Para resolver uma inequação trigonometrica devemos procedir com o processo de transformação exactamente como na resolução de equações trigonometricas.
Daí que, \(sen x=-\frac{1}{2}\) \(\Rightarrow sen x=sen (\pi+\frac{\pi}{6}) \vee sen x=sen (-\frac{\pi}{6})\) \(\Rightarrow x=\frac{7\pi}{6} +2k\pi \vee x=-\frac{\pi}{6}+2k\pi \), com \(k \in Z\).

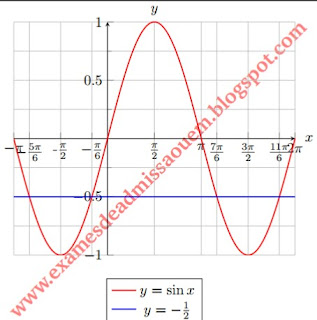
Agora vamos esboçar os gráficos de \(y=sen x\) e \(y=-\frac{1}{2}\) no mesmo sistema cartesiano ortogonal.

Atraves do gráfico podemos ver que \(sen x\ge -\frac{1}{2}\) quando \(x \in [-\pi ; -\frac{5\pi}{6}]\cup [-\frac{\pi}{6}; \frac{7\pi}{6}]\cup [\frac{11\pi}{6}; 2\pi]\).

17. A soma \(1+\frac{4}{3}+\frac{5}{3}+2+\frac{7}{3}+\frac{8}{3}+3+...+124+\frac{373}{3}+\frac{374}{3}+125\) é igual a:

Resolução:
Ao analisarmos a sequência acima podemos concluir que ela pode ser escrita da seguinte forma: \(\frac{3}{3}+\frac{4}{3}+\frac{5}{3}+\frac{6}{3}+\frac{7}{3}+\frac{8}{3}+\frac{9}{3}+...+\frac{372}{3}+\frac{373}{3}+\frac{374}{3}+\frac{375}{3}\) \(=\frac{3+4+5+6+7+8+9+...+372+373+374+375}{3}\).
Agora vamos achar a soma no numerador, pois os seus termos constituem uma \(P.A.\), onde \(a_1=3\) e \(d=1\).
Mas como a fórmula da soma dos primeiros \(n\) termos de uma \(P.A.\) é dada por \( S_n=\frac{(a_1+a_n)n}{2}\), então primeiro precisamos de calcular o valor de \(n\) atraves da fórmula do termo geral de uma \(P.A\).
\(a_n=a_1+(n-1)d\)
Assim, como 375 e o valor correspondente ao último termo, teremos:
\(375=3+(n-1)\cdot 1\) \(\Rightarrow 375=3+n-1\) \(\Rightarrow n=375-2\) \(\Rightarrow n=373\).
Agora ja temos todos os dados necessarios para acharmos a soma no numerador: \(S_373=\frac{(3+a_373)373}{2}\) \(\Rightarrow S_373=\frac{3+375)373}{2}\) \(\Rightarrow S_373=70497\).
Depois vamos divivir pelo denominador, isto é, por 3: \(\frac{70497}{3}=23499\).

18. O valor máximo da função \(f(x)=x^3-3x^2 \) no intervalo \([-1;4]\) é:

Resolução:
Para acharmos os extremos (máximo ou mínimo) de uma função primeiro devemos encontrar a primeira derivada dessa função.
\(f(x)=x^3-3x^2\) \(\Rightarrow f'(x)=3x^2-6x\).
Em seguida vamos determinar os zeros da primeira derivada, pois os zeros da primeira derivada são os extremos de função dada.
Assim, \(3x^2-6x=0\) \(\Rightarrow 3x(x-2)=0\) \(\Rightarrow 3x=0 \vee x-2=0\) \(\Rightarrow x=0 \vee x=2\).

Agora vamos elaborar a tabela de variação de sinal da primeira derivada de modo da encontrarmos a monotonia da função \(f(x)\), e consequentemente o ponto máximo no dado intervalo.
TABELA
Entretanto, o valor máximo é \(f(0)=0\).

19. Determine o valor mínimo do domínio da função \(y=\sqrt{x-\frac{1}{x}}\).

Resolução:
Para determinar o valor mínimo do domínio desta função primeiro vamos encontrar o seu domínio. Tratando-se de uma função irracional fraccionaria, então o radicando (o que está dentro da raíz) não deve ser negativo, isto é, de ser maior ou igual a zero.
Daí que: \(x-\frac{1}{x}\ge 0\).
Agora vamos transformar esta inequação de modo a termos um unico termo no primeiro membro.
\(x-\frac{1}{x} \ge 0\) \(\Rightarrow \frac{x^2-1}{x} \ge 0\)
Em seguida vamos achar os zeros do numerador.
\(x^2-1=0\) \(\Rightarrow x^2=1\) \(\Rightarrow x=\pm \sqrt{1}\) \(\Rightarrow x=\pm 1\).
E como o radicando é uma fracção com variavel no denominador então o denominador deve ser diferente de zero, isto é, \(x\ne 0\),

Com estes \(3\) valores de \(x\) vamos elaborar uma tabela para acharmos os intervais que satisfazem a inequação.

20. Seja \(h\) uma função cujo gráfico tem um ponto máximo de abcissa \(x=2\). Qual dos seguintes gráficos poderá representar o da primeira derivada de \(h\)?

Resolução:
Os zeros da primeira derivada de uma função são os extremos desse mesma função. Assim, \(x=2\) é zero da primeira derivada de \(h(x)\), neste caso as alternativas \(A\) e \(C\) são as que tem \(x=2\) como zero de função. Mas ainda não sabemos qual delas tem um ponto máximo nesse extremo.
Para determinar se um ponto é máximo ou mínimo devemos avaliar o sinal da primeira derivada:
1) Se \(h'(x)\) é negativa a esquerda do ponto \(x=2\) e positiva a direita então \(x=2\) é mínimo.
2) Se \(h'(x)\) é positiva a esquerda do ponto \(x=2\) e negativa a direita então \(x=2\) é máximo.

Como nós queremos determinar o ponto máximo, então vamos verificar qual dos gráficos obdece a condição 2). Entretanto, é o gráfico da alternativa \(C\).